Next Nest

wusa!~(•㉨•)

「稽古】左偏紅黑樹 O 二叉查找樹與（二叉）平衡樹的簡易開啓方式

发表于 Valine：

之前筆者簡單談過了二叉樹的基礎構造與遍歷相關操作，這回我們稍微説一説二叉樹的簡易應用——二叉查找樹，以及其進階——（二叉）平衡樹。

Intro

二叉查找樹1 (Binary Search Tree，簡稱BST)，是一類對節點與其左右孩子關係具有約束的二叉樹的統稱。
其最明顯的性質是如若該樹不爲空，則其 任何節點的值大於其左孩子的值、小於其右孩子的值 （反之即左孩子>本體>右孩子亦然，但一般很少反過來定義，因爲效果其實沒什麽兩樣）。
基於這一性質，我們能明顯地看出來這樣一棵樹的中序遍歷是遞增的，因此這也經常作爲一種有序數據結構，用於對元素的排序。

（二叉）平衡樹 (Balanced Tree，簡稱BT)，是一類對節點數量加以約束的二叉查找樹的統稱。
這一類查找樹的特點在於會盡量避免查找樹某個節點一側的節點量過大、節點過多，從而在某些極端情況下也能避免查找時的時間複雜度過高。

BST

二叉查找樹的簡介。

二叉查找樹是一種樹形數據結構，滿足以下特徵：

  1. 空樹是二叉查找樹；
  2. 任何節點的值（如若左孩子存在）大於其左孩子的值、（如若右孩子存在）小於其右孩子的值；
  3. 正如二叉樹是遞歸定義的一樣，二叉查找樹也是遞歸定義的一樣——二叉查找樹的左右子樹也是二叉查找樹，也滿足相關性質。

因爲二叉查找樹本質上也是二叉樹，沒有需要特殊結構才能實現的功能，因此其節點的定義與二叉樹是一樣的：

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct Node {
    int val;
    struct Node *parent, *lchild, *rchild;
} *root;
struct Node * new_node(int _value) {
    // 類比高級語言中的對象構造函數並加以簡單封裝。
    // 除了指向母親節點與左右孩子的指針外，目前的節點結構中沒有除了`val`之外其他的成員，
    //  因此此處初始化中，僅需要對`val`進行賦值。
    struct Node * q = (struct Node *)malloc(sizeof(struct Node));
    q->val = _value;
    q->lchild = nullptr;
    q->rchild = nullptr;
    q->parent = nullptr;
    return q;
}

使用結構體數組模擬的靜態實現、使用Python等高級語言的對象引用機制的實現當中的定義與上面的相似，於此不再贅述。
因此二叉查找樹的遍歷也與普通的二叉樹相仿，在此列舉出先序遍歷與中序遍歷的方法。

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void __preorder(struct Node *rt) {
    if (rt != nullptr) {
        printf(" %d,", rt->val);
        __preorder(rt->lchild);
        __preorder(rt->rchild);
    }
}
void __inorder(struct Node *rt) {
    if (rt != nullptr) {
        __inorder(rt->lchild);
        printf(" %d,", rt->val);
        __inorder(rt->rchild);
    }
}
void printall() {
    __preorder(root);   putchar('\n');
    __inorder(root);    putchar('\n');
}

Searching

作爲二叉查找樹，其與應用最爲直接相關的功能即爲search。
根據性質3知道我們可以遞歸遍歷二叉查找樹以尋找所求值，性質2決定遍歷時每一步的方向，性質1用於部分情況的判斷。
大致的思路如下：

  • 如若這個節點==nullptr，則以其為根的樹是空樹，所以遍歷到該節點後，便找不到所求的_target值，此時返回nullptr以表示在樹上不存在帶有所求值得節點；
  • 如若當前節點帶有的值即爲所求，即返回當前節點的位置；
  • 如若當前節點帶有的值!=所求值，則
    • 所求值<當前節點帶有的值->在左子樹中繼續尋找，
    • 所求值>當前節點帶有的值->在右子樹中繼續尋找。
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct Node * __search(struct Node *rt, int _target) {
    if (rt == nullptr)
        return nullptr;
    else if (_target == rt->val)
        return rt;
    else {
        if (_target < rt->val)
            return __search(rt->lchild, _target);
        else
            return __search(rt->rchild, _target);
    }
} inline bool search(int _target) {
    return __search(root, _target) != nullptr;
}

在這裏我們容易看出，函數__search返回的是帶有值_target的節點所在的位置，然後函數search通過審察該位置是否存在節點以判斷樹中是否存在所求的值_target。

Insertion

二叉查找樹所模擬的是一個集合，因此其中所有的元素如若存在，則唯一。
爲了保證這一點，我們再插入之前應當先判斷行將插入的元素是否已經存在於該樹當中，如若不存在，則再插入它。

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct Node * __insert(struct Node *rt, int _value) {
    if (rt == nullptr)
        return new_node(_value);
    else {
        if (rt->val != _value) {
            if (_value < rt->val) {
                rt->lchild = __insert(rt->lchild, _value);
                rt->lchild->parent = rt;
            } else {
                rt->rchild = __insert(rt->rchild, _value);
                rt->rchild->parent = rt;
            }
        }
        return rt;
    }
} inline void insert(int _value) {
    root = __insert(root, _value);
}

以上過程中，遞歸的每一步中，函數__insert返回的是節點rt本身的位置，這個返回過程像是在確認 我就是我，我的左孩子就是我左下方那位、有孩子就是我右下方那位 一樣，這個過程會在後面涉及到旋轉操作的平衡樹中用到。

Rotation

一般而言只有在部分平衡樹中會用到的操作，旋邊。
但筆者對二叉查找樹的刪除操作進行了優化，其中可能會用到，故於此進行簡單講解。
由於筆者在構思時出了一點錯誤，所以關於該方法，在此暫不進行講述。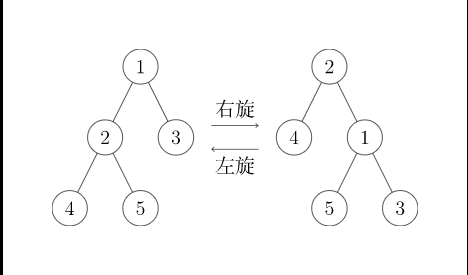

二叉樹的旋邊是針對邊(edge)進行的操作，分爲左旋和右旋兩種。

旋邊有一條非常重要而且好用的性質，那就是：旋邊不改變中序遍歷順序！
這一點很容易看出來，其相關證明筆者不在此贅述。

Left Rotate

如上圖，左旋是對某一個節點及其右孩子進行的操作。
左旋時，連接節點與其右孩子的邊逆時針旋轉，使節點成爲原本右孩子的左孩子，而後接管其左孩子，使之成爲自己的右孩子。

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct Node * rotate(struct Node *rt) {
    /**
     * Left Rotate an Edge...
     *        [1]               [2]
     *        / \               / \
     *       *  [2]    ==>    [1]  *
     *          / \           / \
     *         O   *         *   O
     */
    Node * newroot = rt->rchild;
    if (newroot != nullptr) {
        // 處理被旋邊所連接的兩個節點指向母親與孩子的指針。
        rt->rchild = newroot->lchild;
        newroot->lchild = rt;
        newroot->parent = rt->parent;
        rt->parent = newroot;
        // 如若需要接管的孩子不爲空，則更新其指向母親節點的指針。
        if (rt->rchild != nullptr)
            rt->rchild->parent = rt;
        return newroot;
    }
}

於是，當我們需要左旋連接節點node及其右孩子的邊的時候，如下形式調用函數rotate即可完成旋邊操作：

C++
1
node = rotate(node);

Right Rotate

右旋操作與上方左旋操作類似。

C++
1
2
3
4
5
6
7
8
9
10
11
12
struct Node * rotrev(struct Node *rt) {
    Node * newroot = rt->lchild;
    if (newroot != nullptr) {
        rt->lchild = newroot->rchild;
        newroot->rchild = rt;
        newroot->parent = rt->parent;
        rt->parent = newroot;
        if (rt->lchild != nullptr)
            rt->lchild->parent = rt;
        return newroot;
    }
}
C++
1
2
// For Instance ...
node = rotrev(node);

Removing

二叉查找樹的刪除操作需要在進行的時候維持相關的性質。
對於部分二叉查找樹，刪除過程會被特化爲兩種，一種是如同對優先隊列進行pop操作的刪除最小值remove_min，另一種是刪除指定值，即remove。

對於待刪除節點，由於二叉樹、二叉查找樹都是遞歸定義的數據結構，所以往往需要維護其左右子樹在該節點被刪除后不破壞二叉查找樹的性質。
對於樸素二叉樹，此時要考慮左子樹是否存在、右子樹是否存在兩個相互獨立的問題所組成的四種情形：

  1. 左右子樹皆不存在：待刪除節點為一片葉子：此時的解決方案便是直接刪除該節點，無需考慮左右子樹的維護問題；
  2. 右子樹不存在，待刪除節點有且僅有左子樹：此時的解決方案便是使左孩子取代待刪除節點，若待刪除的并非根節點，便由母親節點接管其左子樹；
  3. 僅左子樹不存在的情況，可以類比如上方法；
  4. 左右子樹皆存在，此種情況的處理較爲複雜。傳統的處理便是保留其左子樹，使其右孩子取代待刪除的節點，即把右孩子的值複製到待刪除節點上，然後遞歸刪除右孩子（保留右子樹並以左孩子進行取代亦可）。但筆者在此想到一種方案，便是把同時具有左右子樹的節點通過旋邊變成僅僅具有左子樹的節點，實現其的操作便是左旋連接待刪除節點與其右孩子的邊。旋邊後待刪除節點會携左子樹移動到原本左孩子的位置上，而原本的右孩子成爲待刪除節點的母親節點。如若原本的右孩子的左子樹不爲空，則會由待刪除節點接管并成爲其右子樹，此時則繼續旋邊，直到待刪除節點不具有右子樹爲止。然後如2.中所言，以其左孩子取代待刪除節點即可。

具體程式筆者在此不再贅述。

BT

何爲平衡？爲何平衡？在考慮這些問題之前請讓我們先審察一種情形：

當我們從某時起，向二叉查找樹加入的元素總是加入在上一個加入的元素下方，從某一個節點開始便會只具有左孩子或右孩子，從而形成一條“長鏈”。
此時的二叉查找樹中以某一個節點為根的子樹便會退化為一條綫性表（鏈表），極端不理想情況下，沿著那一條“長鏈”遍歷的時間複雜度便會升至O(m)。
如若能夠控制從根節點出發的每一條路徑長度都大致相等，則不理想情況下，遍歷的時間複雜度也能控制在O(log m)左右。
由此便引入二叉查找樹中的一個重要概念，那便是，平衡。

我們可以先感性地理解一下：所謂平衡樹便是每個節點左右子樹大致相當的二叉查找樹。
但對於不同種類的平衡樹，其所定義的平衡也不一樣，以下將簡單介紹兩種常見的二叉查找樹的平衡：

  1. 弱平衡（期望平衡）：多見於Treap2或Splay3；
  2. 高度平衡：多見於AVL4平衡樹，其核心在於任意節點的左右子樹高度差不超過一。

References

筆者引用的一些參考文獻，以及希望給出的一些相關資料與題目，供大家輔助參考理解二叉查找樹與平衡樹的相關概念。