Next Nest

wusa!~(•㉨•)

「稽古】左偏紅黑樹 II 紅黑樹的節點與神乎其技的旋邊

发表于 Valine：

之前講解了紅黑樹通過維持“黑高平衡”以實現倍數平衡的原理，但是

維護紅黑樹的性質是比較複雜的。如果我們要插入一個節點：首先，它一定會被染色成紅色，否則會破壞黑高平衡。縱使這樣，還有可能會出現連續的兩個紅色節點。因此需要進行調整。而刪除節點就更加麻煩，與插入類似，我們不能刪除黑色節點，否則會破壞黑高的平衡。

Intro

爲了解決這樣的問題，我們引入一個Robert Sedgewick所提出的容易實現的方案：左偏紅黑樹1（Left-Leaning Red-Black Tree，簡稱LLRBT，又稱左傾紅黑樹或左斜紅黑樹）。

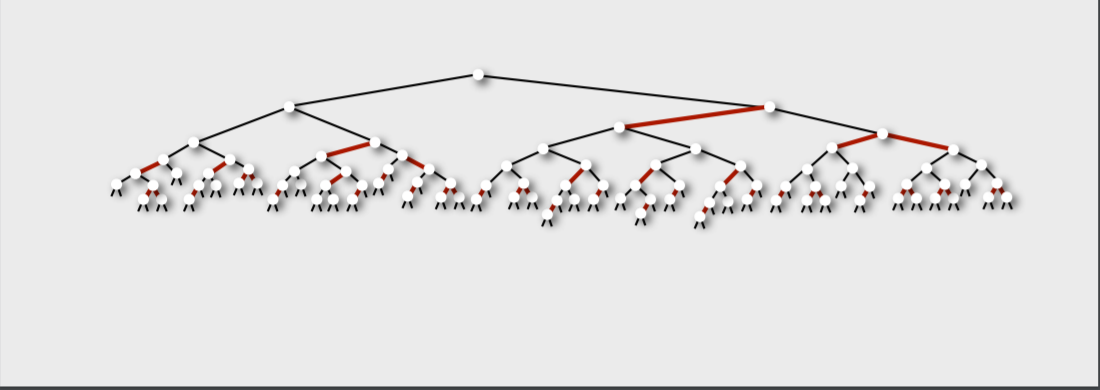
在左偏紅黑樹中有一點與紅黑樹不同，那便是左偏紅黑樹中是邊具有顔色而非節點具有顔色，但我們爲了表示方便，用一條邊中的孩子來表示該邊的顔色。

左偏紅黑樹對紅黑樹進行了進一步限制，一個黑色節點的左右孩子滿足以下特徵：

  1. 要麽全爲黑色（即從一個黑色節點延展出兩條黑邊）；
  2. 要麽左孩子為紅色而右孩子為黑色。

這兩點保證了所有的紅邊都是左偏的，即紅邊只會連接某個節點與其左孩子，而不是右孩子。
由此可以看出，這是一種特殊的紅黑樹，這些新加入的特徵對其進行限制，使其增刪操作可以與2-3-4樹3構成一一對應。
可以通過一下一正一反兩個例子來理解這兩條特徵：

  • 符合條件的情形
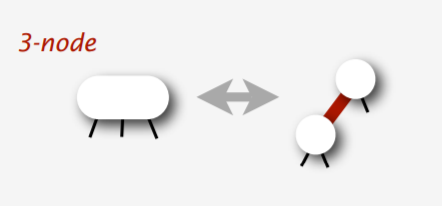
  • 不符合條件的情形

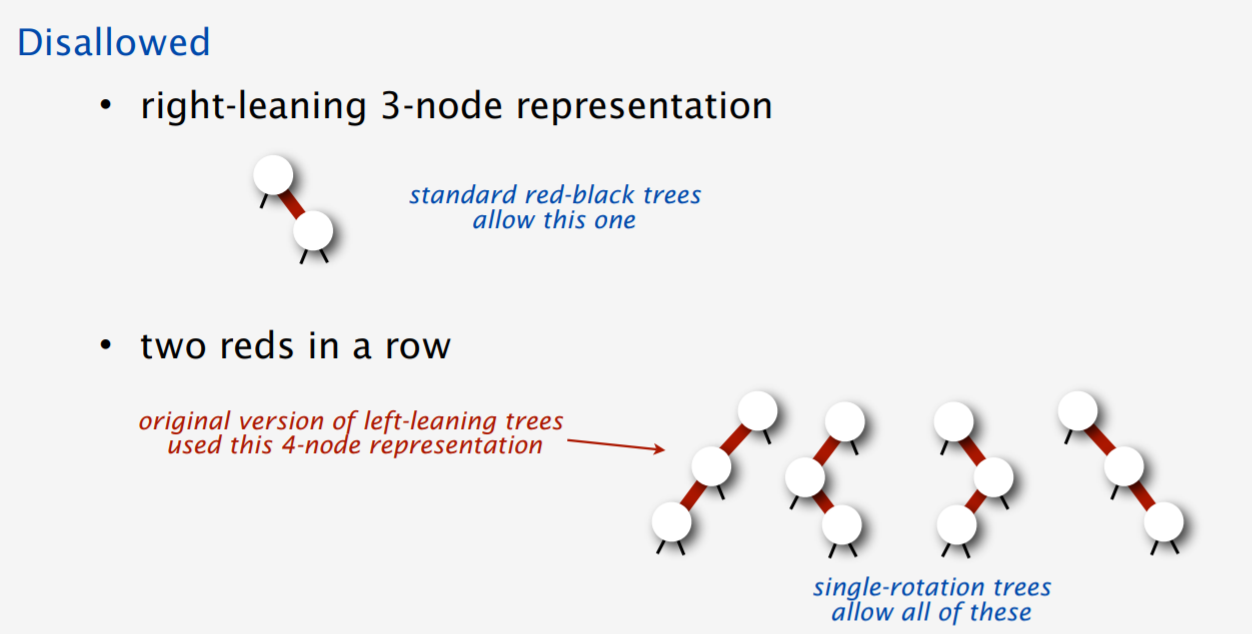
Structure

左偏紅黑樹中，在二叉查找樹的結構基礎之上，我們將加入一個成員colored以記錄某個節點的染色情況。
黨colored為真時，我們視這個節點為紅色節點，亦即連接其與其母親節點的邊為紅邊，否則視爲黑邊。
如此這般便有了左偏紅黑樹中節點的基本結構：

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct Node {
    int val;
    struct Node *parent, *lchild, *rchild;
    bool colored;
} *root;
struct Node * new_node(int _value) {
    // 類比高級語言中的對象構造函數並加以簡單封裝。
    struct Node * q = (struct Node *)malloc(sizeof(struct Node));
    q->val = _value;
    q->lchild = nullptr;
    q->rchild = nullptr;
    q->parent = nullptr;
    // 在創建節點時預先染紅，關於這一點將在後面進行解釋。
    q->colored = true;
    return q;
}

Rotation

對於左偏紅黑樹的節點，旋邊時其他的與普通的二叉查找樹的旋邊操作無異，但需要注意兩個節點染色情況的改變。
以左旋爲例，原本的孩子會取代母親的位置，繼承其母親與祖母相連的邊的顔色，在表示上便是該點被更新爲其母親的染色情況；而原本的母親將會被旋轉至其孩子的位置，表示該邊染色情況的節點從原本的孩子變爲旋轉成爲孩子的母親，效果上也是繼承其孩子的染色情況…右旋也是類似的過程。
如若能夠理解以上過程，那麽我們可以發現紅黑樹（不僅是左偏紅黑樹）的旋邊中染色情況的變化可以簡單概括爲：被旋邊兩端節點染色情況交換。

  • 左旋 Left Rotate
    • 代碼
      C++
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      struct Node * rotate(struct Node *rt) {
          /**
          * Left Rotate an Edge...
          *        [1]               [2]
          *        / \               / \
          *       *  [2]    ==>    [1]  *
          *          / \           / \
          *         O   *         *   O
          */
          Node * newroot = rt->rchild;
          if (newroot != nullptr) {
              // 先進行常規的旋邊過程。
              rt->rchild = newroot->lchild;
              newroot->lchild = rt;
              newroot->parent = rt->parent;
              rt->parent = newroot;
              if (rt->rchild != nullptr)
                  rt->rchild->parent = rt;
              // 而後交換兩節點染色情況。
              swap(rt->colored, newroot->colored);
              return newroot;
          }
      }
    • 例
      C++
      1
      node = rotate(node);
  • 右旋 Right Rotate
    • 代碼
      C++
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      struct Node * rotrev(struct Node *rt) {
          Node * newroot = rt->lchild;
          if (newroot != nullptr) {
              rt->lchild = newroot->rchild;
              newroot->rchild = rt;
              newroot->parent = rt->parent;
              rt->parent = newroot;
              if (rt->lchild != nullptr)
                  rt->lchild->parent = rt;
              swap(rt->colored, newroot->colored);
              return newroot;
          }
      }
    • 例
      C++
      1
      node = rotrev(node);

Flip

紅黑樹中還有一個重要操作，便是顔色的翻轉，其可以使某節點及其左右孩子的染色變爲與當前相反的情況。

C++
1
2
3
4
5
inline void flip(struct Node *rt) {
    rt->colored = !(rt->colored);
    rt->lchild->colored = !(rt->lchild->colored);
    rt->rchild->colored = !(rt->rchild->colored);
}

Extra

事實上，紅黑樹本身就是與2-3-4樹等價的，我們可以從nullzx的這篇文章4裏這兩張圖中理解這一點：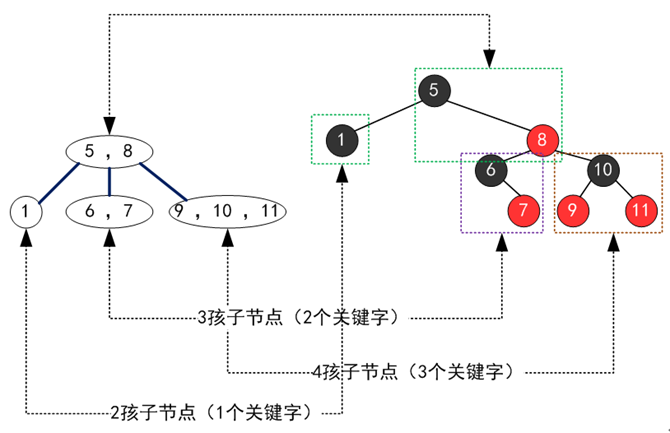

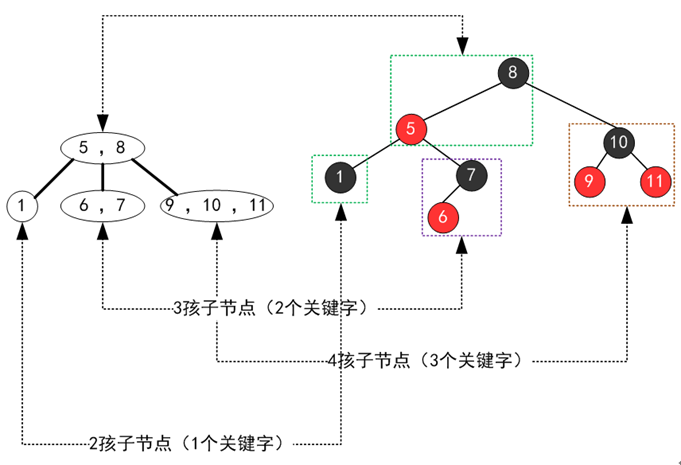
由於左偏紅黑樹不存在右偏的紅邊，所以可以認爲對應的2-3-4樹中不存在4-節點，因此可以認爲左偏紅黑樹等價於2-3樹：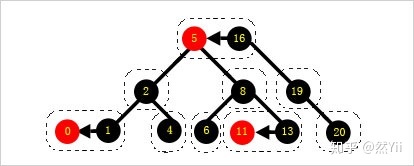

References

1. OI-Wiki章節 左偏紅黑樹 ↩
2. Left-Leaning Red-Black Trees, Robert Sedgewick, Princeton University ↩
3. Algorithms - Balanced Search Trees, Robert Sedgewick, Kevin Wayne ↩
4. nullzx的博客園文章 从2-3-4树到红黑树（中） ↩