Next Nest

wusa!~(•㉨•)

「稽古】左偏紅黑樹 III 插入節點的修正方法

发表于 Valine：

現在已經先後講完了二叉查找樹的基本增刪操作，左偏紅黑樹的概念與結構特徵，以及旋邊、翻轉操作。
需要的前置内容已經全部理清，現在可以開始審察其節點插入操作。

Intro

左偏紅黑樹1節點的插入操作可以理解爲在常規地二叉查找樹插入後，修復插入後的左偏紅黑樹，以保證其仍然滿足左偏紅黑樹的相關特徵。
由於隨意插入黑色節點會頻繁破壞黑高平衡，使維護工作難度變大，因此我們在插入節點的時候 默認插入的是紅色節點， 然後在修復的過程中再進行染色調整。
由於紅黑樹中本身存在兩種節點：紅色節點與黑色節點，因此在插入的時候我們也分爲向黑色節點插入與向紅色節點插入兩種情形進行討論。

Insertion

into Black Nodes

如圖，向黑色節點的插入操作可以分爲插入為左孩子與插入為右孩子兩種情形。
前者情形由於插入的節點目前為葉子，且其母親節點向上的邊為黑邊，而在過程中沒有破壞左偏紅黑樹的相關特徵，因此不必再進行維護操作；後者情形會使被插入的母親節點延展出一條右偏的紅邊，此時需要把這條右偏的紅邊進行左旋使其左偏，以維護左偏紅黑樹的相關特徵。

into Red Nodes

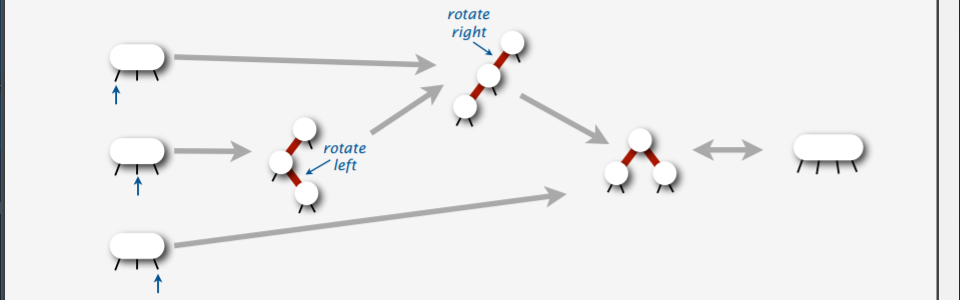
如圖，向紅色節點的插入操作可以分爲插入為紅邊左孩子的左孩子、插入為紅邊左孩子的右孩子與插入為紅邊母親節點的右孩子三種情形，根據原作者在文獻中的講解，我們先考慮把前兩者轉化爲第三種情形。

把前兩者轉化爲第三種情形，我們通常采用的手段是：先把第二種情形轉化爲第一種，再把第一種情形轉化爲第三種。
把第二種情形轉化爲第一種的方法很簡單，如同插入為黑色節點的右孩子一樣，把連接插入的節點與其母親節點的右偏紅邊左旋即可。
第一種情形中，會出現兩條連續的左偏紅邊，此時需要操作被插入的母親節點以及其母親，使上方的左偏紅邊右旋，被插入的母親節點把原本的母親節點接管為自己的右孩子，並以右偏的紅邊進行連接。

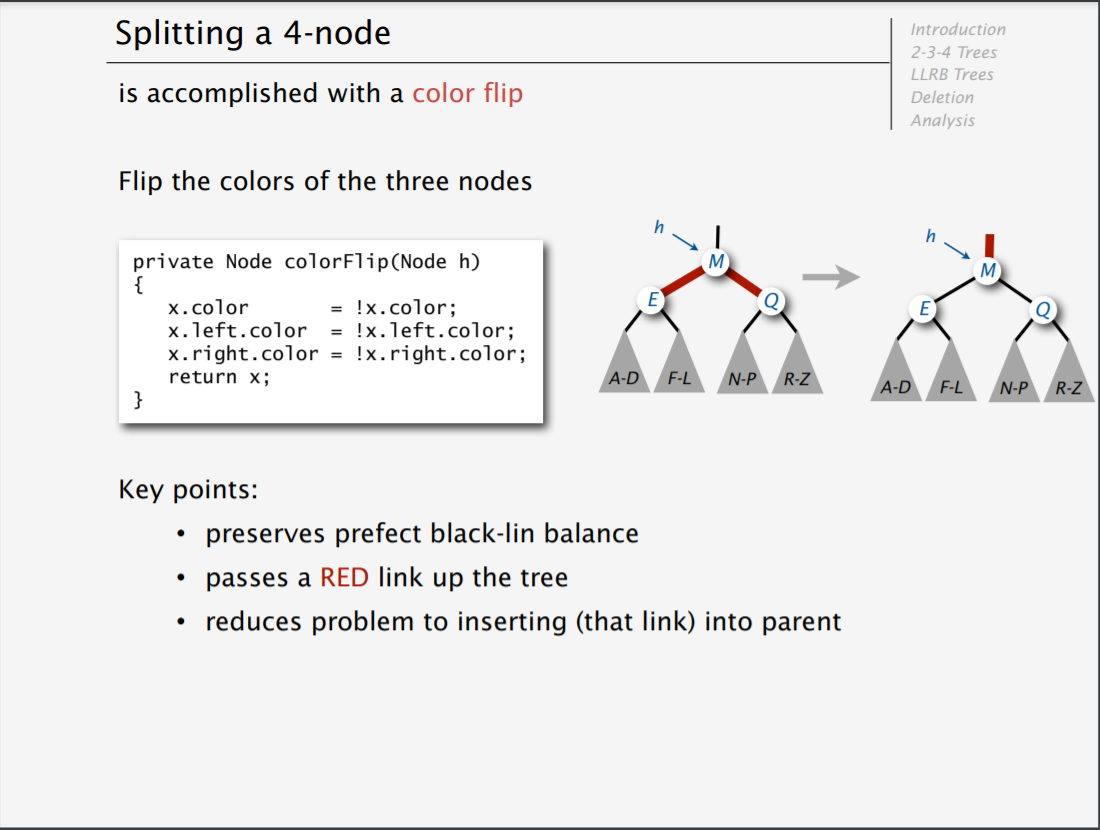
當我們把前兩者都轉化爲第三種情形後，還需要對第三種情形進行處理，這是因爲第三種情形中被插入的母親節點延展出了一條右偏的紅邊。
但此時的處理也很簡單，根據紅黑樹的性質，母親節點向上的一定為黑邊，此時可以通過flip翻轉操作，把兩條紅邊連接孩子們、一條黑邊向上連接的節點變爲兩條黑邊連接孩子們、一條紅邊向上連接的節點，從而消滅右偏紅邊（把其轉化爲右偏黑邊）的同時維持局部的黑高平衡。

Solution

讓我們稍微總結並整合一下上述的插入過程。
這是原作者Sedgewick在原文ppt2上最初的總結：

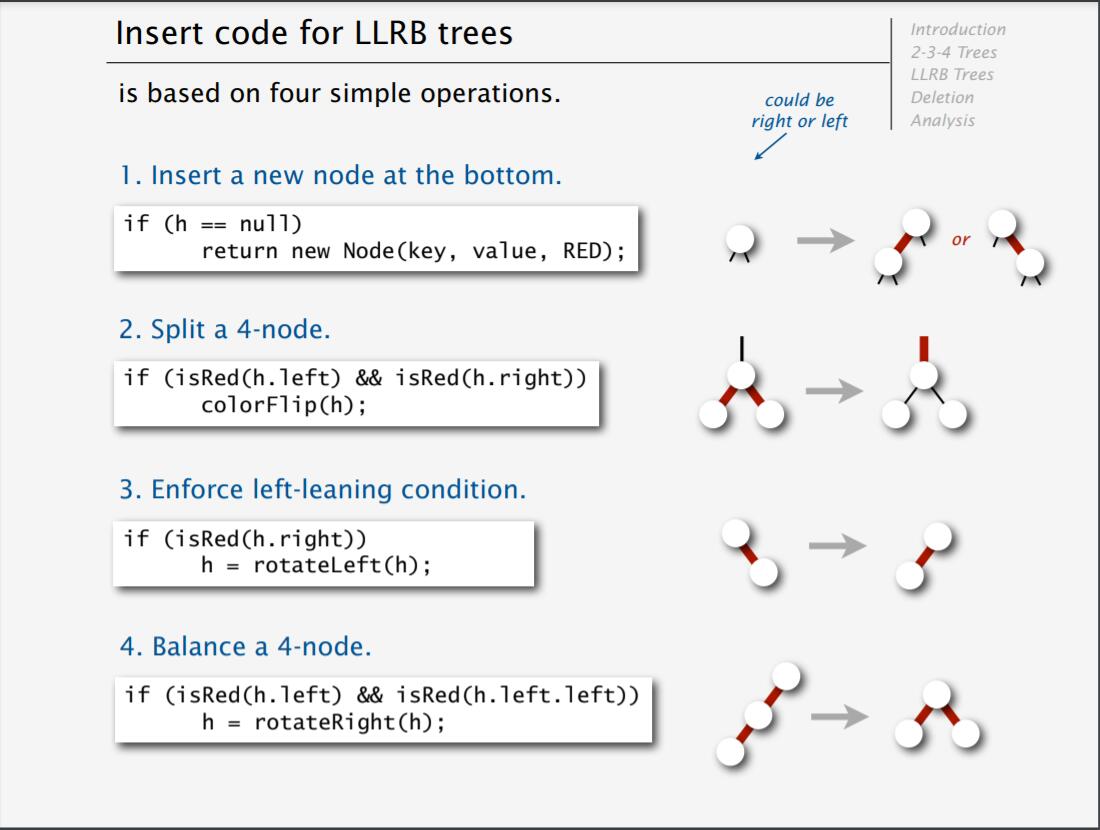
我們先處理與4-節點等價的由某個節點延展出的左右兩條紅邊，通過翻轉顔色消滅右偏紅邊的同時把原本左偏的紅邊上移，實質上等價於把2-3-4樹中的一個4-節點分裂為兩個2-節點。

如若不屬於上述情況，則考慮下面的過程：在插入紅色節點之後，我們先把插入的右孩子左旋，如若產生了兩條連續紅邊，再左旋為延展出左右兩條紅邊的，與4-節點等價的節點。

但這樣做在最後無疑會遺留新的4-節點，於是後面Sedgewick把分裂4-節點的操作移到最後，以保證不會遺留4-節點：

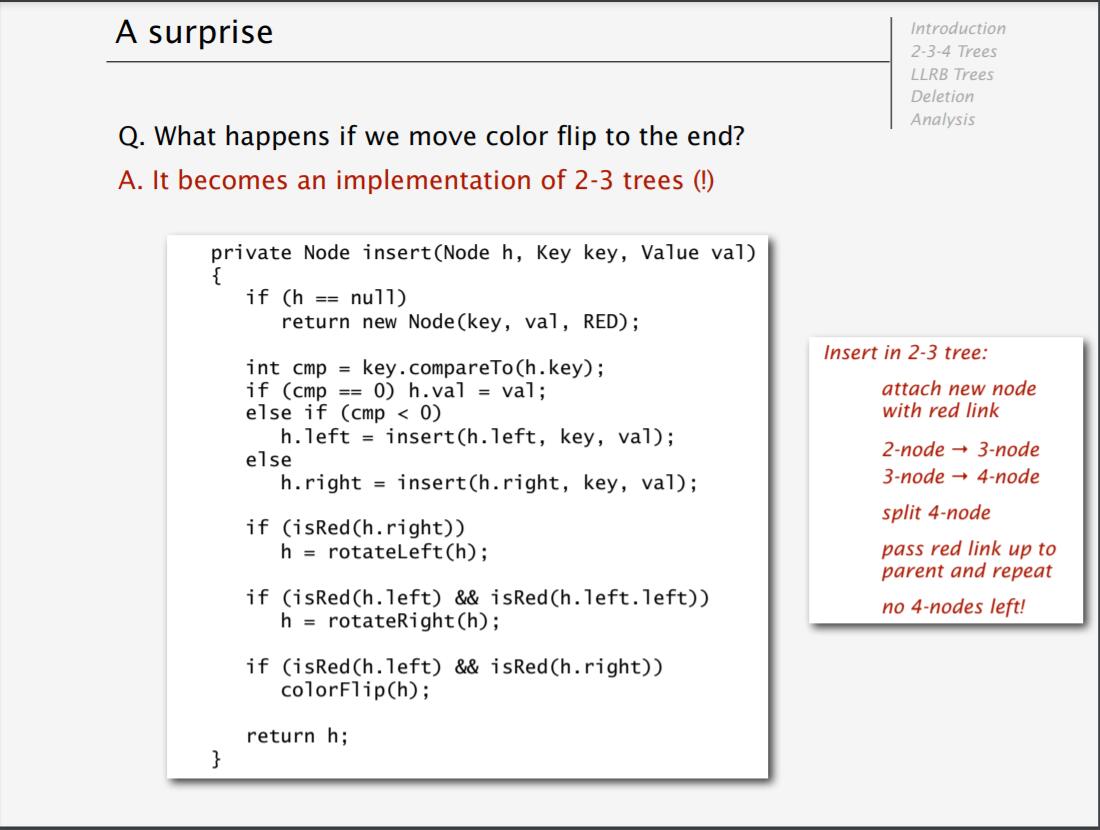
從程式上看就像是對普通的二叉查找樹的插入操作加入了幾行修正的操作。

Program

我們可以把這些操作，簡單地封裝一下。

Color Judgement

首先我們需要一個可以在某個節點非空的基礎之上判斷其是否被染色的函數：

C++
1
2
3
inline bool judge_colored(struct Node *rt) {
    return (rt != nullptr) ? (rt->colored) : false;
}

Fix Up

然後是封裝插入過程中的修正過程，因爲後面可能還會用到：

C++
1
2
3
4
5
6
7
8
9
10
11
struct Node * fixup(struct Node *rt) {
    if (judge_colored(rt->rchild))
        rt = rotate(rt);
    if (judge_colored(rt->lchild)
     && judge_colored(rt->lchild->lchild))
        rt = rotrev(rt);
    if (judge_colored(rt->lchild)
     && judge_colored(rt->rchild))
        flip(rt);
    return rt;
}

Insertion Process

於是插入過程可以寫如下：

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
struct Node * __insert(struct Node *rt, int _value) {
    if (rt == nullptr)
        return new_node(_value);
    else {
        if (rt->val != _value) {
            if (_value < rt->val) {
                rt->lchild = __insert(rt->lchild, _value);
                rt->lchild->parent = rt;
            } else {
                rt->rchild = __insert(rt->rchild, _value);
                rt->rchild->parent = rt;
            }
        }
        // 最後一步，普通的二叉查找樹便是直接返回節點`rt`，但我們這裏要...
        return fixup(rt);
    }
} inline void insert(int _value) {
    root = __insert(root, _value);
    // 修正過程的最後可能會把根節點染色，在這裏我們要强制把它的顔色進行修正
    root->colored = false;
}

Tree-Printing

此外，爲了清晰地表示節點的染色情況，我們稍微修改了一下二叉樹的printall函數：

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void __preorder(struct Node *rt) {
    if (rt != nullptr) {
        if (rt->colored)
            printf(" [%d],", rt->val);
        else
            printf("  %d ,", rt->val);
        __preorder(rt->lchild);
        __preorder(rt->rchild);
    }
}
void __inorder(struct Node *rt) {
    if (rt != nullptr) {
        __inorder(rt->lchild);
        if (rt->colored)
            printf(" [%d],", rt->val);
        else
            printf("  %d ,", rt->val);
        __inorder(rt->rchild);
    }
}
void printall() {
    __preorder(root);   putchar('\n');
    __inorder(root);    putchar('\n');
}

References

1. OI-Wiki章節 左偏紅黑樹 ↩
2. Left-Leaning Red-Black Trees, Robert Sedgewick, Princeton University ↩