一點簡短的convlstm筆記

如題，是一份slides。
等有空整理出來。

Download

~~其實真寫出來感覺學過的人不用看，給沒學過的人看也沒講清楚。~~

Intro

ConvLSTM¹是由 Xingjian Shi 博士提出的深度學習模型。其定義是遞進的，為了說明什麼是ConvLSTM，筆者將會先後淺談以下幾個模型：

FC (Full Connection, 全連接層)
RNN (Recurrent Neural Network, 循環神經網絡)
LSTM (Long-Short Term Memory, 長短期記憶網絡)
ConvLSTM

但之所以要從FC倒著講回ConvLSTM，原因在於：
ConvLSTM是LSTM中使用卷積運算代替矩陣乘法的模型，
LSTM是RNN中引入「細胞狀態」的模型，
RNN是FC對時間序列特化形成的模型，
而FC是神經網絡的基礎結構。

FC

FC的全稱為 Full Connection ，是意為全連接層的結構。
最為早期的神經網絡是輸入、輸出矢量，矢量中的每一個分量在網絡中根據不同的加權，進行線性組合形成新的矢量。

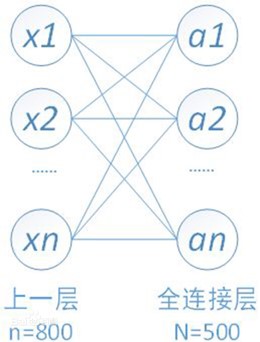
以上圖為例，當我們輸入矢量 $x = (x_1, x_2, \cdots, x_n )^\mathrm{T}$ 之後，矢量x會經過如下變換：

$\left \{ \begin{aligned} a_1 & = & w_{1,1}x_1 & + & w_{1,2}x_2 & + & \cdots & + & w_{1,n}x_n, \\ a_2 & = & w_{2,1}x_1 & + & w_{2,2}x_2 & + & \cdots & + & w_{2,n}x_n, \\ & & & & & & \vdots & & \\ a_m & = & w_{m,1}x_1 & + & w_{m,2}x_2 & + & \cdots & + & w_{m,n}x_n \end{aligned} \right.$

亦即：

$a_k = w_{k,1}x_1 + w_{k,2}x_2 + \cdots + w_{k,n}x_n = \sum_{l=1}^n w_{k,l}x_l , (k = 1, 2, \cdots , m)$

上式可以表示為矩陣乘法：

$\vec{a} = W\vec{x}$

在上圖中對應著的超參數 m=500, n=800 ，分別為輸出節點數（矢量維數）與輸入節點數（矢量維數），亦是權重矩陣W的尺寸。
但全連接層在使用時除了權重矩陣W外，也會常常結合偏置矢量(bias)b與激勵函數²(activation)f使用，此時真正的輸出為：

$\vec{a} = \psi(W\vec{x} + \vec{b})$

關於偏置矢量與激勵函數，筆者在此暫不贅述。

RNN

在考慮何為LSTM之前讓我們先明確一下RNN。
眾所周知RNN是一種機器學習模型，用於處理時間序列，這裡的時間順序不僅可以是傳統意義上的時間順序，也可以認為是藉由因果關係串聯而成的事情發展順序。

例如「隨著某課程章節推進，每一章作業量所組成的序列」，在此選取的每個元素即「每一章節的作業量」所對應的時間間隔並不均勻（課程中講解重點的章節所花費的時間遠比一般的章節要長），所以此處的「時間」為課程中章節的推進而非傳統的年月日時分秒等…

而RNN是為了方便處理時間序列而對FC進行優化後的機器學習模型，其引入了一個非常重要的「時間」維度，並以一個單獨的矢量存儲每一時刻的狀態。

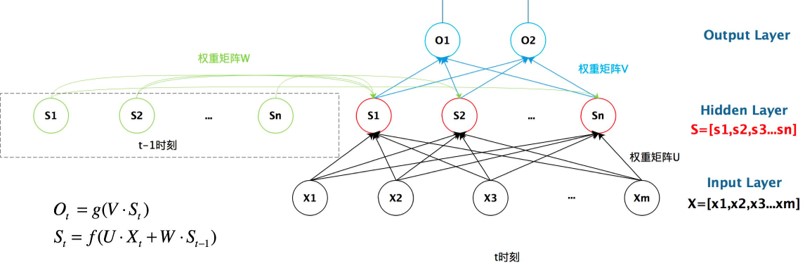
剛才提到全連接層的實質就是矩陣乘法，那麼從上圖我們可以看到權重矩陣 U, W, V 形成了三個以全連接層為基礎的結構。

現在我們來解釋為什麼RNN是FC對時間序列的「特化」：

$\left \{ \begin{aligned} \vec{o_t} & = g(V\vec{s_t}), \\ \vec{s_t} & = f(U\vec{x_t} + W\vec{s_{t-1}}) \end{aligned} \right.$

我們可以看到比起FC，RNN在中間插入了一個隱藏層，其對應著矢量 $\vec{s_t}$ ， $\vec{s_t}$ 同時受 $\vec{s_{t-1}}$ 與 $\vec{x_t}$ 的影響，這便是隨著t不斷變化，這便是用於存儲「時間」狀態的變量。

同時我們可以看出，FC輸入時接收的是一個矢量 $\vec{x}$ ，而RNN輸入的時候接收的是多個矢量組成的序列 $\vec{x_1}, \vec{x_2}, \cdots, \vec{x_T}$ 。

根據前面講過的式子，對於每一個時刻t，都會根據 $\vec{s_t}$ 產生相應的 $\vec{o_t}$ ，這也對應著每一個時刻相應的輸入 $\vec{x_t}$ 。

如何理解？

我們先來看一例由Keras實現的FC：

Python

>>> import keras
>>> model = keras.Sequential([
    keras.layers.Dense(
        units = 128,
        input_shape = (32,),
        ),
    ])
>>> model.summary()

通過調用.summary()查看其結構：

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense_1 (Dense)              (None, 128)               4224
=================================================================
Total params: 4,224
Trainable params: 4,224
Non-trainable params: 0
_________________________________________________________________

再看一例由Keras實現的SimpleRNN

Python

>>> import keras
>>> model = keras.Sequential([
    keras.layers.Embedding(10000, 32),
    keras.layers.SimpleRNN(
        units = 128,
        return_sequences = True,
        ),
    ])
>>> model.summary()

通過調用.summary()查看其結構：

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, None, 128)         20608
=================================================================
Total params: 340,608
Trainable params: 340,608
Non-trainable params: 0
_________________________________________________________________

相比於FC的輸出形狀(None, 128)，RNN的輸出形狀(None, None, 128)中間多了一個None分量，代表著每次RNN不像FC一樣只輸出一個矢量，其輸出的也是一個矢量序列，且該矢量序列的長度可以不固定。

所以我們可以看出，不同於對輸入的一個矢量進行處理的FC，RNN是對輸入的一個矢量序列進行處理的模型，其中存在著以（隨時間變化）矢量 $\vec{s_t}$ 用於存儲模型隨時間的狀態改變，這是RNN能夠處理時間序列的結構基礎。

雖然RNN輸入的是一個矢量序列，但如若只需要最後時刻的結果，其輸出的也可以只是輸出的矢量序列中最後一個，相當於捨棄了前面的 $\vec{o_1}, \vec{o_2}, \cdots, \vec{o_{T-1}}$ 從而只保留 $\vec{o_T}$ 一個矢量。

Keras也可以實現只返回最後一個輸出向量的RNN：

Python

>>> import keras
>>> model = keras.Sequential([
    keras.layers.Embedding(10000, 32),
    keras.layers.SimpleRNN(
        units = 128,
        return_sequences = False,
        ),
    ])
>>> model.summary()

通過調用.summary()查看其結構：

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
embedding_2 (Embedding)      (None, None, 32)          320000
_________________________________________________________________
simple_rnn_2 (SimpleRNN)     (None, 128)               20608
=================================================================
Total params: 340,608
Trainable params: 340,608
Non-trainable params: 0
_________________________________________________________________

LSTM

LSTM的誕生來源於在表示時間狀態的向量 $\vec{h_t}$ 不斷變化時，輸入時刻靠前的輸入向量的特徵較早吸收，但會被後來者「沖淡」。
為了解決這一問題，保證靠前的輸入向量的特徵也能較好地吸收，LSTM應運而生。

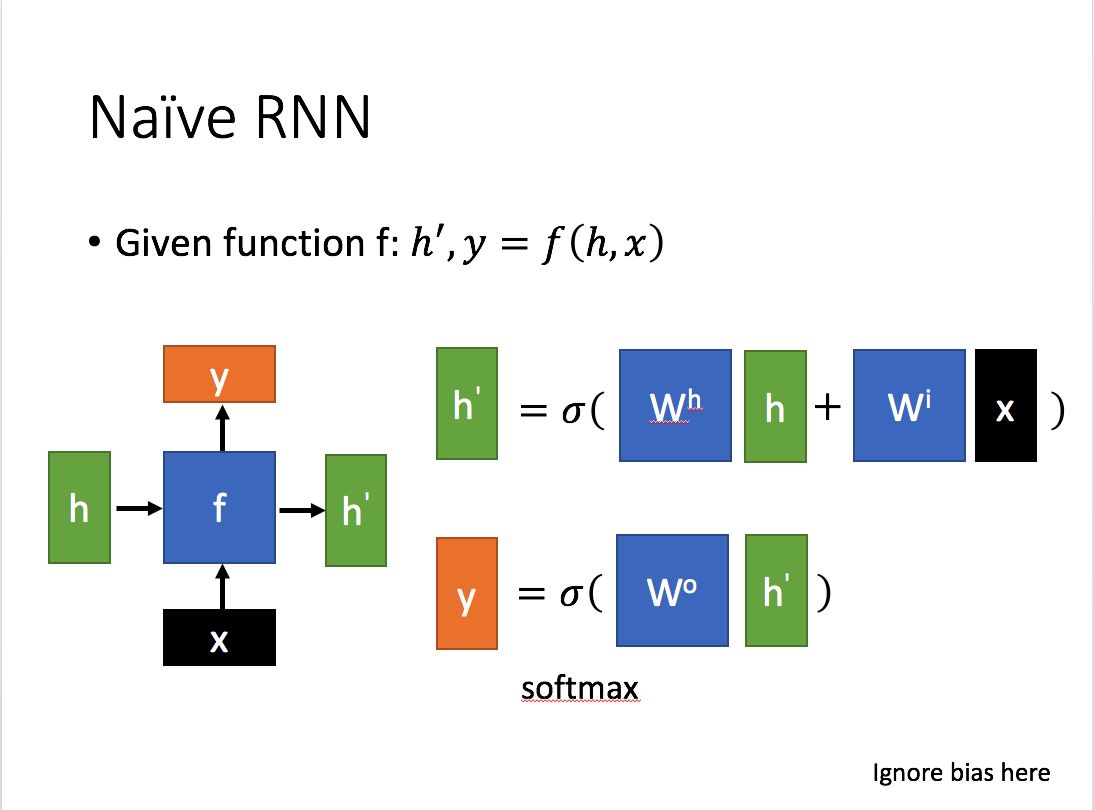
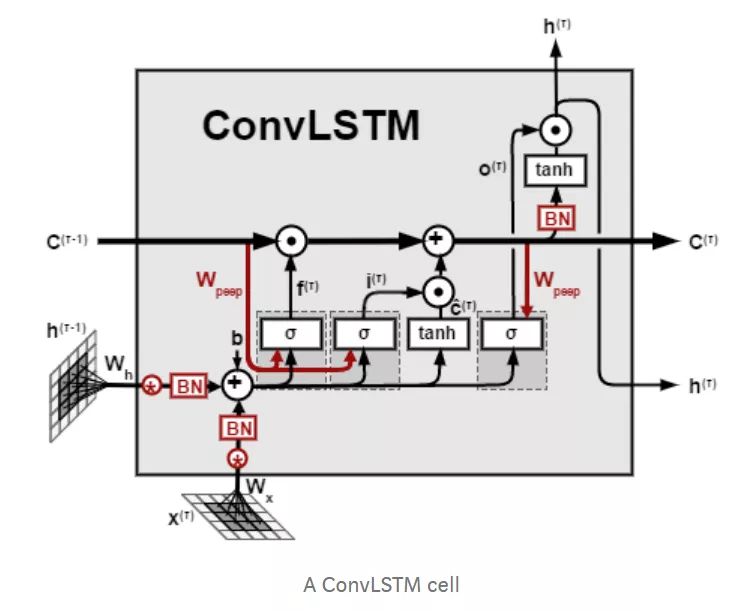
解決的方式很簡單， $\vec{h_t}$ 是一個不斷接收上一時刻 $\vec{h_{t-1}}$ 與此時刻輸入向量 $\vec{x_t}$ 的狀態向量，那麼我們引入一個與之不同，只隨著上一時刻的 $\vec{c_{t-1}}$ 變化、不直接接收此時的輸入向量 $\vec{x_t}$ 的另一個狀態向量 $\vec{c_t}$ 即可。

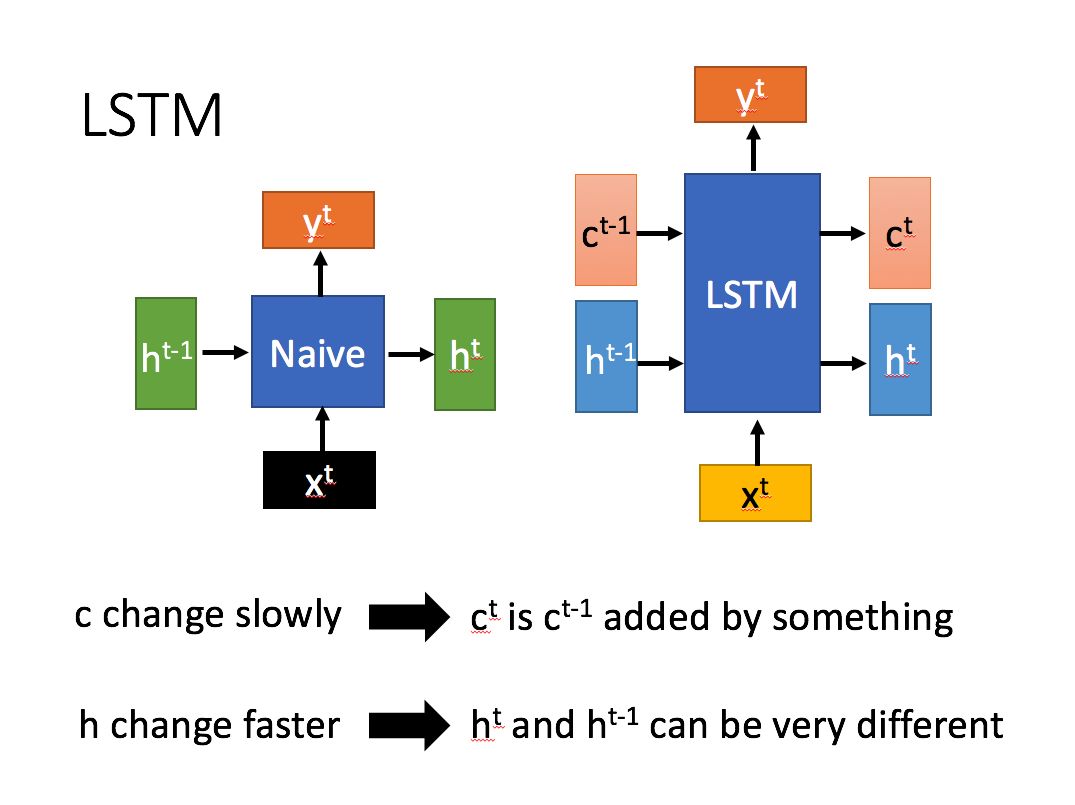
從圖中我們可以看到 $\vec{c_t}$ 為 $\vec{c_{t-1}}$ 吸取經過處理的 $\vec{h_{t-1}}$ 與 $\vec{x_t}$ 的特徵而不斷迭代的狀態向量，而 $\vec{h_t}$ 的每一次迭代為根據 $\vec{h_{t-1}}$ 與 $\vec{x_t}$ 的重構，其迭代過程遠比 $\vec{c_t}$ 的要復雜，因此變化也比 $\vec{c_t}$ 要劇烈，變化更快。
不同於 $\vec{c_t}$ 變化緩慢，帶有的記憶更長， $\vec{h_t}$ 所帶有的記憶更短，變化更快。
這是LSTM能夠同時記住近期與早期輸入數據特徵，使靠前的輸入向量的特徵也能較好吸收的關鍵結構。

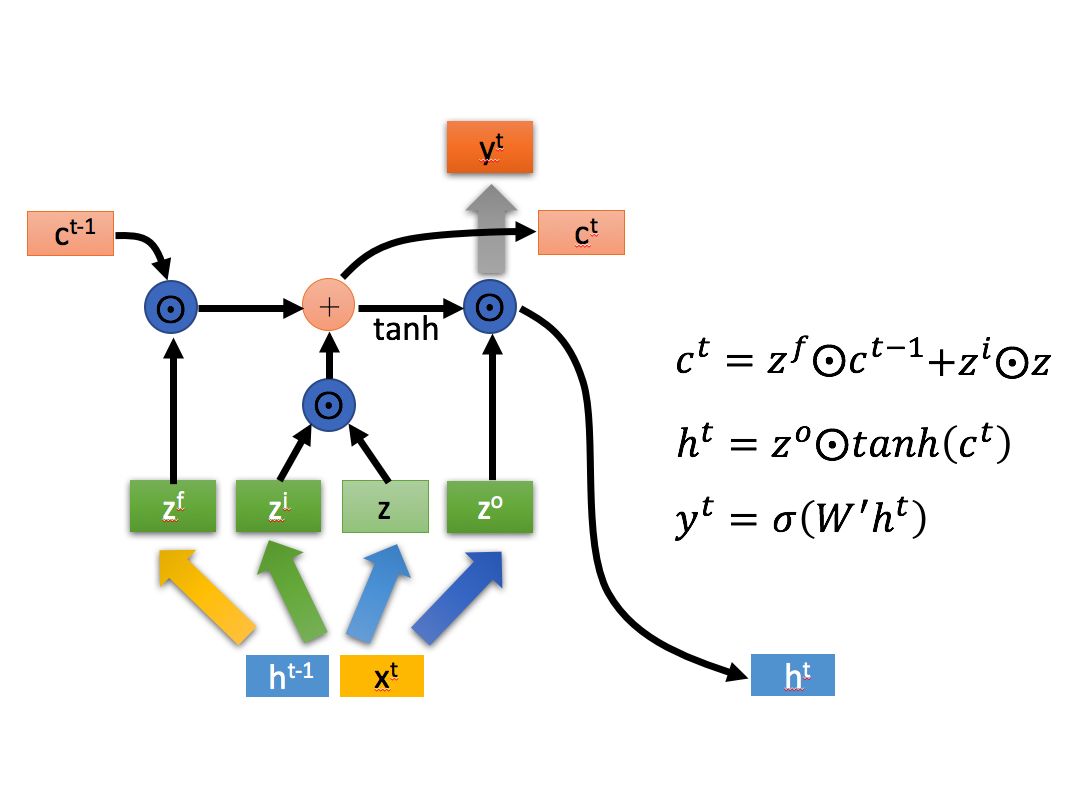
整理一下：

$\vec{h_t}$ 的變化所受因素更多，迭代程度更劇烈、迭代速度更快，構成LSTM的短期記憶；
$\vec{c_t}$ 的變化所受因素較少，迭代程度不明顯、迭代速度更慢，構成LSTM的長期記憶。

所以這個模型被稱為 Long-Short Term Memory ，長短期記憶網絡。

ConvLSTM

在進入LSTM之前，我們先看一看卷積(Convolution)，一種特殊的矩陣間乘法運算。
雖然說是乘法運算，但對於參與卷積運算的兩個矩陣，其兩者位置不能隨意交換。
因為卷積運算可以視為由尺寸較小的一個矩陣在尺寸較大的矩陣上「取樣」，把不同位置取到的結果根據相對位置關係排列為新的矩陣。
我們看如下的動圖簡單理解一下：

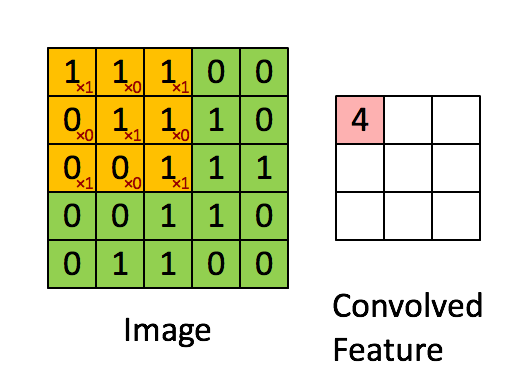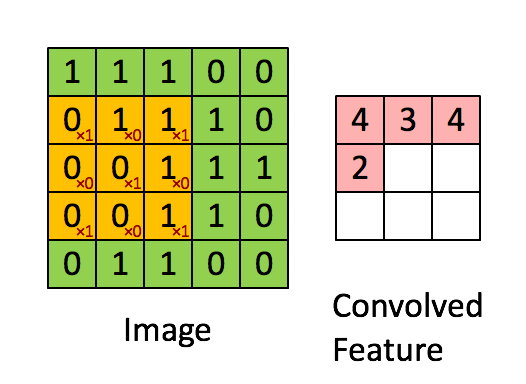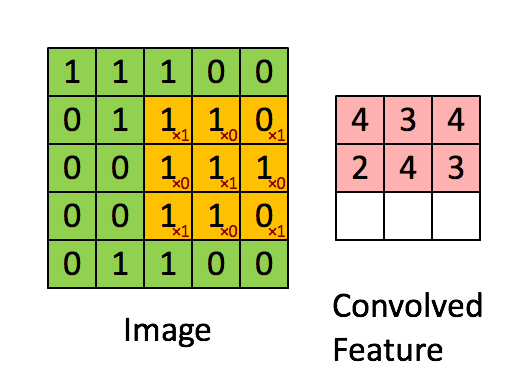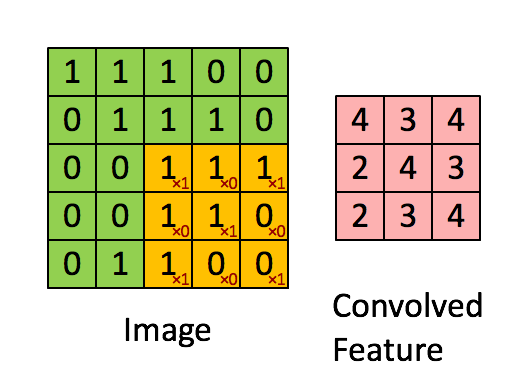
當我們的輸入為向量序列的時候，每一時刻輸入模型的是該時刻的向量，在進行乘法的時候直接使用矩陣乘法即可，但是矩陣乘法的實質（於右位而言）是對矩陣中不同列的線性變換與組合，無法提取不同行之間的相關特徵，因此在輸入為矩陣序列而非向量序列的時候，我們使用卷積替代傳統的矩陣乘法。

References

¹. X. Shi, Z. Chen, H. Wang, D.-Y. Yeung, W.-K. Wong, and W.-C. Woo, “Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting”, 2015, arXiv: 1506.04214 ↩

². 百度百科詞條激活函數 ↩